
I like the HashMap, it’s is one of my favorite data structures and amazingly fast.
Peg solitaire java 64 Bit#
The next step is to use the brute force approach: 64 bit JVM and the -d64 option to activate the 64 bit mode.

Peg solitaire java 32 bit#
Increasing the heap size with the well known -Xmx does not help on a 32 bit JVM: The memory needed does not fit into the 32 bit address space. Starting this without any JVM options results in an OutOfMemoryError, the HashMap does not fit into the standard heap. This sounds very promising, so let’s try the next board size, n = 7. That’s about 270,000 times faster compared to the sequential solver and even 67,500 times faster compared to the parallel solver running with four cores. For n = 6 we get a more impressing effect, only 0.4 seconds elapse before we can see the result. For n = 5 this doesn’t make a big difference, we get the answer in 0.07 seconds, 70% of the time needed by the simple sequential solver. As a precondition, the class Board has to implement hashCode() and equals(). This is a well known technique called transposition table. An obvious optimization is to store the number of solutions for already computed positions in a HashMap. CachingĪs in most board games, there is often more than one sequence of moves which result in the same position. So let’s look for some other optimizations. I assume it would exceed the lifetime of the poor machine.

So why bother? Four cores, four times faster than sequential, perfect speedup.īut what about n = 7? How many solutions are there for a board with edge length seven? I didn’t run this on my laptop, neither sequential nor parallel. Compared to the 30 hours of the sequential solver, a factor of four, which matches the number of “real” cores. Starting this, my laptop (eight cores with hyperthreading, four real ones) was unusable for the next 7 hours and 28 minutes. After some experiments I used eight as threshold in my test runs. This avoids the overhead of task creation for small problems. I introduced another optimization (as proposed in the fork/join tutorial): The parallel algorithm switches back to a sequential one when there are less than sequential pegs left. The recursion of the sequential algorithm has been replaced by the creation of new instances of RecursiveTask.
Peg solitaire java code#
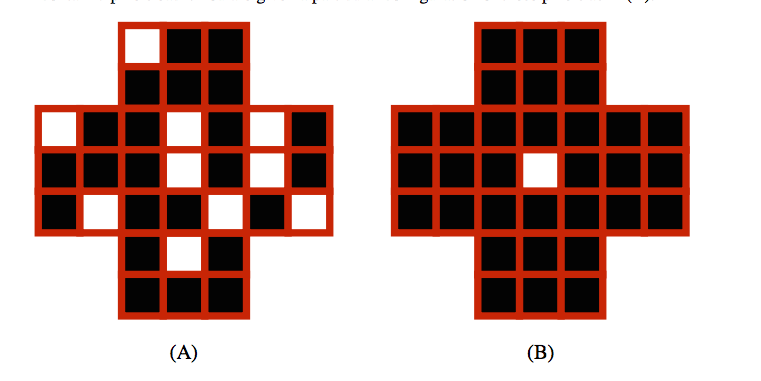
Given a Java class which can represent a position and which is capable to compute a list of all resulting positions after one move, the solver is a simple recursive function ( source code as zip): You get different results for different starting positions, see Dan O’Briens Puzzle Solution Page for some more information on the topic. So the board could look like this after one move: xĪ solution is found when there is only one peg left, wherever it is located on the board. The leapfrogged peg is removed from the board. A legal move is a jump over one peg in one of the six different directions. The middle peg of the third row is empty. A board with edge length 5 (n = 5) before any move has been done looks like this: x Lets start with a more precise definition of the problem. You may be surprised to find other techniques are much more efficient for these problems. The problem to solve is: How many different solutions exist for a board with n pegs on a side? The focus is on different optimization techniques, not only the Fork/Join framework. In this article, I use a simple board game as an example for a parallel algorithm and other optimization techniques, a variant of peg solitaire. Even modern smartphones often have four cores. To utilize these modern beasts, you need parallel programming. On the other hand, the number of cores increases: Laptops with eight cores are common (okay, including hyperthreading, only four real cores). In the last few years there has been nearly no improvement in single thread performance of CPUs.


 0 kommentar(er)
0 kommentar(er)
